Coordinate Geometry
Coordinate Geometry
Coordinate Geometry
Equation of a line
- y = mx + c, where m = gradient and c = y intercept (when x = 0)
- This is given in the formula booklet
Gradient
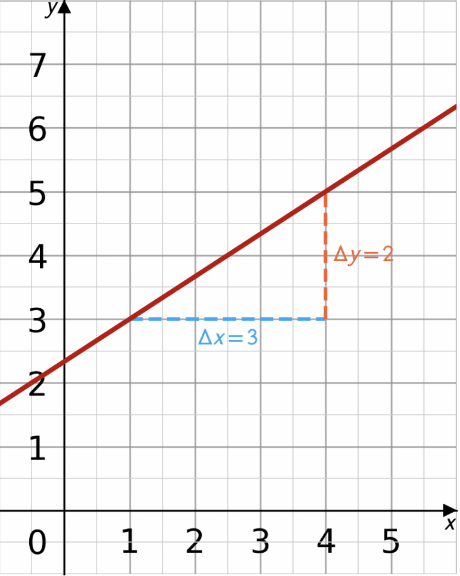
- The gradient of a line which increases its y value as its x value increases is positive (as seen below)
- The gradient of a line which decreases its y value as its x value increases is negative
- Formula: Rise divided by Run = (y2-y1)/(x2-x1). By doing so, you will find the displacement, which essentially is the "rise" and the "run". You can see below, that the rise is 2, and the run is 3, so its gradient is 2/3.
- This formula can be found in the formula booklet
Perpendicular lines
- You will often be asked to find the gradient of a line perpendicular to line ____.
- Simply divide –1 (negative one) with the gradient of the line they give you, and you will find the gradient of the perpendicular line.
Exam Tips
Note that this formula is not given in the formula booklet, so it is useful to memorize it.
Intersection of 2 lines
- Two lines will intersect at one point as long as they are not parallel (have same gradient) or identical (same gradient and same y intercept)
- To find the point of intersection, make one equation of the line equal to the other equation of the line, effectively eliminating y.
- Then, solve for x. After finding the x value, plug it into any of the equations to find the y value where both lines intersect. You know have the coordinates of the intersection.
Distance between 2 lines in a 3D model
- Use Pythagoras to find the overall displacement. This formula is given in the formula booklet:
- The formula is the same for 2D lines. You simply need to remove the z's from the formula that you are able to calculate the distance between 2 lines in a 2D model
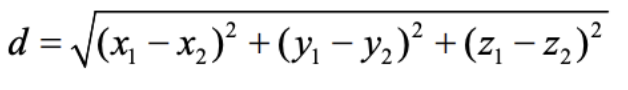
Exam Tips
This type of question is really common. To be able to understand what IB is asking you, draw the shape of the line to be able to fully understand and determine your next steps.

