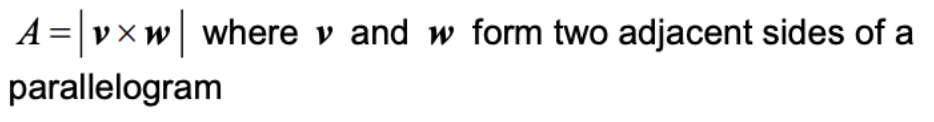Vectors
Vectors
a vector is a direct line segment
Notation
- Vector A (x,y,z), where each letter corresponds to the vector's coordinate
- Position vectors = vectors coming out of an origin
Displacement vector
- Vector AB = Coordinate of point B, also known as position vector, minus the coordinate of point A
Distance between two points
- Formula for magnitude:
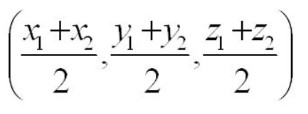
Midpoint between two points
- Formula for magnitude:
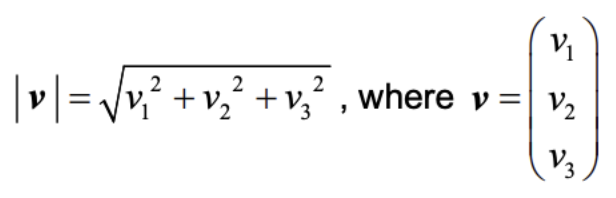
Unit vector
- Vector with a magnitude of 1
- Formula for unit vector: vector A divided by the magnitude of the vector A
- Formula:

Exam Tip
This formula is not given in the formula booklet, so you need to memorize it.
Vector equation of the line
- Formula:
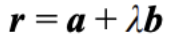
- "a" is any fixed point on the line
- "r" is the position vector of vector R (any point on the line at a chosen λ value)
- d is direction of vector R
Parametric form of the line equations
- This is given in the formula booklet:
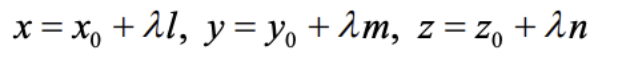
Intersection between 2 lines
- The symbols for λ for the 2 equations are different
- You write the parametric equation for x, y and z, where each parametric equation equals to the dedicated other
- Solve the simultaneous equations to find each value of λ
- Plug the values on the dedicated vector equations of the line to find the point of intersection
Scalar product
- This is given in the formula booklet:
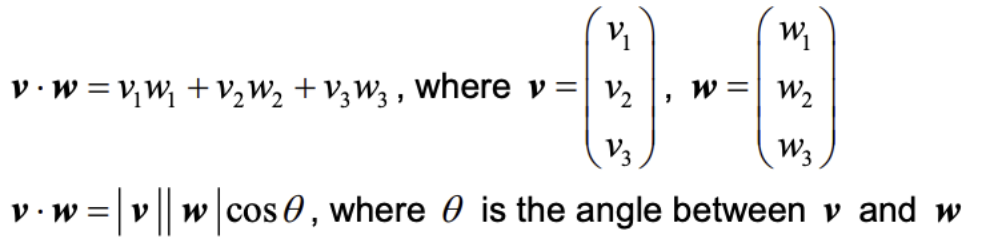
- This is often used when asked about parallel or perpendicular vectors
- If vectors are perpendicular, the scalar product = 0
- If vectors are parallel, the scalar product = 1 or -1
- With this, you can solve for the λ value where the lines are perpendicular (=0)
Angle between 2 lines
- This formula is used to calculate angles between lines, where theta is the angle trying to be solved
- You will be given the magnitude of the vectors and the vectors equations, and you simply need to solve for the angle
- This is given in the formula booklet:
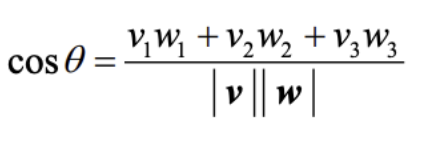
Shortest distance between a point and a line
- To be able to solve this, you will need to use the scalar product formula
- The point where the point is closest to the line is where it is perpendicular to the line
- Solve the scalar product formula with the dedicated values given in the equation and make it equal to 0
- After finding the λ value where the line is perpendicular to the point, plug it into the equation of the line to find the coordinate on the line which is closest to the point
- After that, calculate the displacement vector from the point on the line to the point you are given in the equation, and do the magnitude of that displacement vector. That is the answer for the equation
Exam Tip
Students often forget to calculate the displacement vector after finding the closest point on the line. Remember to do so to earn full marks.
Collision between 2 lines
- The symbols for λ for the 2 equations are the same, and are often called t (for time; used in kinematics)
- You write the parametric equation for x, y and z, where each parametric equation equals to the dedicated other
- Solve the simultaneous equations to find the value of λ
- Plug the value one of the vector equations of the line to find the point of collision
Cross product
- Is a vector that is perpendicular to both vectors
- Formula:
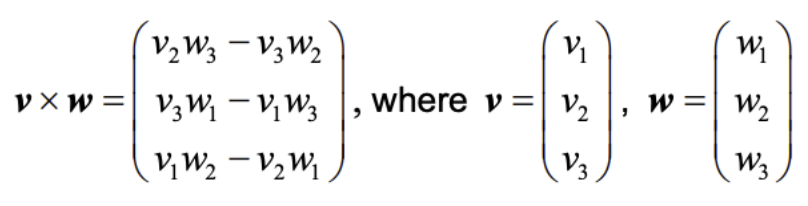
Exam Tip
The formula is given in the formula booklet, but it takes time to calculate, and it is quite tricky, so be careful not to make any silly mistakes
Area of parallelogram and triangles
- Area of a triangle = area of a parallelogram multiplied by 0.5
- Calculate the displacement vectors of any point in the parallelogram and work out its cross product. After that, calculate its magnitude to have your answer.
- Formula: