Matrices
Matrices
Order of a matrix
- The order of a matrix is determined by multiplying the number of rows, n, by the number of columns, m
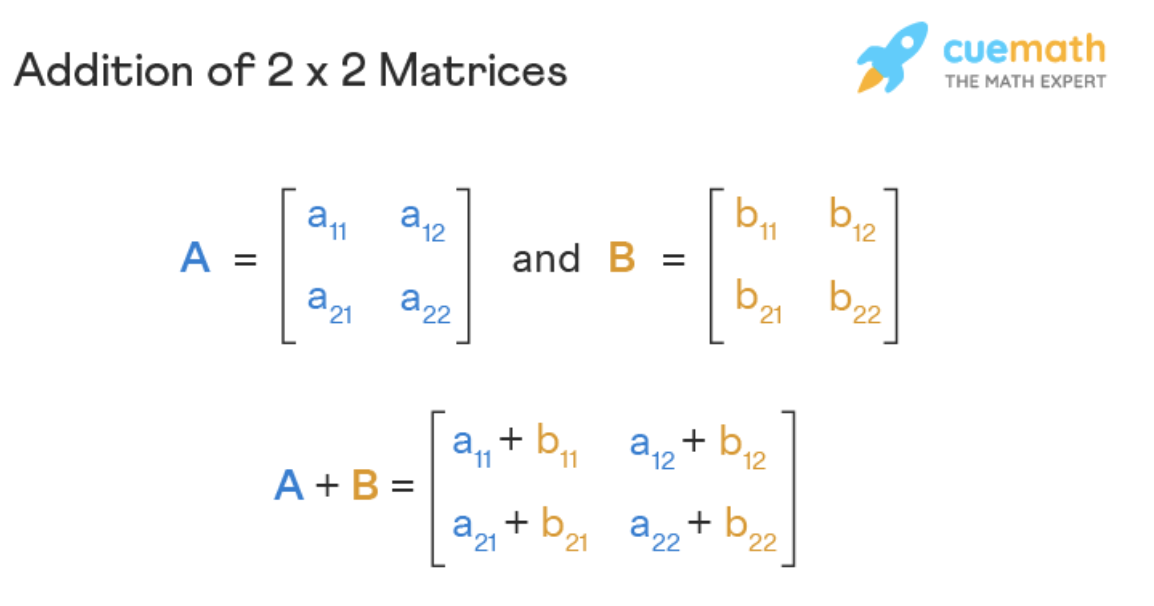
Addition of matrices
- Simply add the values of each position to with the corresponding value in the same position of the other matrix
- Formula for addition:
Subtraction of matrices
- It is the exact same as addition, but you change the operation from addition to subtraction
Identity matrix
- The identity matrix is a matrix where it has a diagonal from the top left to the bottom right of 1's. Multiplying it with any other matrix leaves the other matrix unchanged. It is the same as multiplying a matrix by 1
Properties of matrices
- Matrix multiplication in general cannot be switched
- Matrix multiplication is distributive
- You can place a bracket anywhere, as long as the order of the operations are the same
Determinant of a matrix
- Is found by using the formula given in the formula booklet:
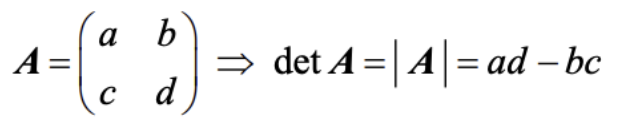
Inverse matrices
- In order to find the inverse of 2 by 2 matrices, you first have to calculate the determinant of the matrix
- After that, you divide 1 by the value found
- Is found by using the formula given in the formula booklet:
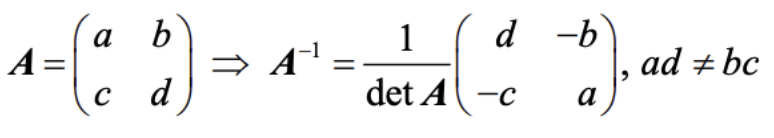
Exam Tip
You are required to show working out when finding the inverse of 2 by 2 matrices. Simply inputting the answer given in the calculator will not yield full marks.
Singular matrix
- A matrix is singular when its det = 0. It does not have an inverse matrix.
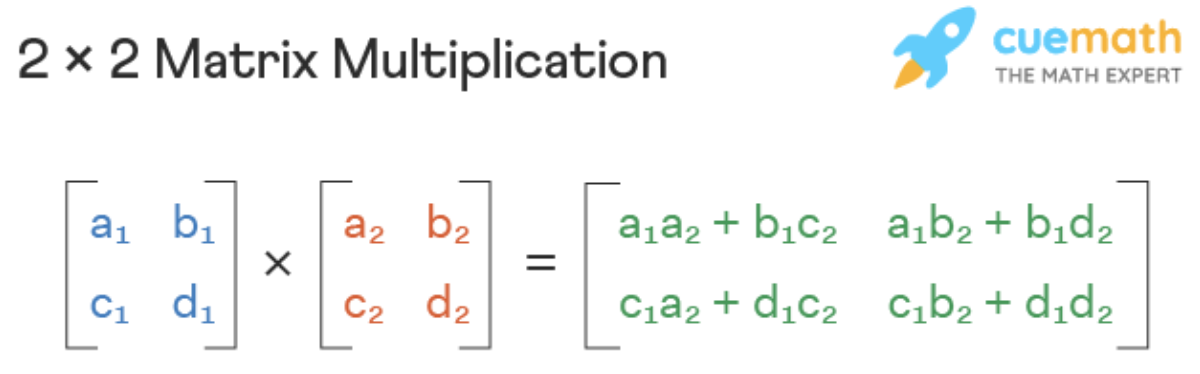
Multiplication of matrices
- In order to multiply matrices, follow the general formula:
Using inverse matrices to find unknowns
- If AB = C, then B = inverse matrix of A x C
- If BA = C, then B = C x inverse matrix of A
- Using this principle, you can find unknown matrices, like C, by using inverse matrices. The equation will be given in the question, and the matrices as well.
Solving system of equations using matrices
- A system of simultaneous equations can be written in matrix form as follows: Ax = B, where x is the matrix of unknowns you will usually be asked to find
- Simply do: Inverse matrix of A x B to find x. You are allowed to use your GDC to do so, just don't forget to show your working out.
Eigenvectors and eigenvalues
- To find the eigen vectors and values of matrix M do:
- Find the determinant of (M- λI), where I is the identity matrix
- After manually finding the values of λ, also known as eigenvalues, plug them in the following equation: M x λ= λ x v, where v is the eigenvector
- Solve for each eigenvalue, finding 2 eigenvectors in total
Power formula for matrices (diagonalization)
- This formula is given in the formula booklet
- Simply find the eigenvalues and eigenvectors of matrix M, and plug them into the formula. After doing so, use your GDC to find the value of the matrix.
- Formula:
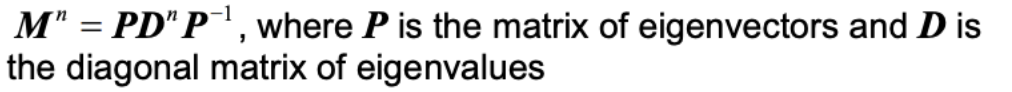
Exam Tip
You are often asked to diagonalize matrices which have unknowns within them. To be able to do so, you must do all by hand, so make sure you are familiar with by-hand multiplication of matrices.

