Functions
Functions
Asymptote
- A vertical asymptote occurs when the denominator is 0
- When there are roots, it cannot be negative. This leads to the graph stopping at that point.
- If a graph of a function approaches but does not reach a horizontal line, it has a horizontal asymptote
Types of relations
- Refers to the number of values each x or y coordinate has; e.g. a linear graph is one to one as there is only one place on the line which has a certain x value, and y value.
- Only one-to-one and many-to-one are functions
One-to-one
- There is only one point which has y = -1 (e.g. -1,-1)
- Example:

Many-to-one
- There are two or more places which have the same y value, but has unique x values for every part of the line
- Example:
One-to-many
- Has unique y values for many possible x values
- Example:

Many-to-many
- Has more than one place with the same x and y value
- Example:

Vertical line test
- To test if you have a function
- Any vertical line crosses the line in only one place (for functions)
Horizontal line test
- To test if a function is one-to-one or many-to-one
- Only crosses the line once if a line is one-to-one
Domain and range of a function
- Domain = the set of inputs (x values)
- Range = the set of outputs (y values)
Graph sketching
Key features
- Y intercepts
- X intercepts
- Roots
- Zeros
- Vertices
Composite functions
- (f ∘ g)(x) = plug function g inside of function f, as if it was the x-value
- (g ∘ f)(x) = plug function f inside of function g, as if it was the x-value
Composite functions
- The domain of the inverse function of f(x) = the range of the function f(x)
- The range of the inverse function of f(x) = the domain of the function f(x)
- The inverse function of f(x) only exists if f is one-to-one on its given domains, otherwise it would be one-to-many, and that is not a function
- The graph of inverse f(x) is the reflection of f(x) in the line y=x
Exam Tip
The output (y value) for the function f(x) is the input for the inverse function f(x) which outputs f(x)'s input. The IB loves to ask these types of questions, so it's nice to have this trick in mind so you can save some time during your exams.
Transformation of graphs
- When one vertical and one horizontal transformation is applied, the order which it is applied does not matter
- When two vertical or two horizontal transformations are applied, the order which they are applied does matter: if dealing with horizontal transformations, you first translate, then stretch. If dealing with vertical transformations, you first stretch, then translate.
- Rules:
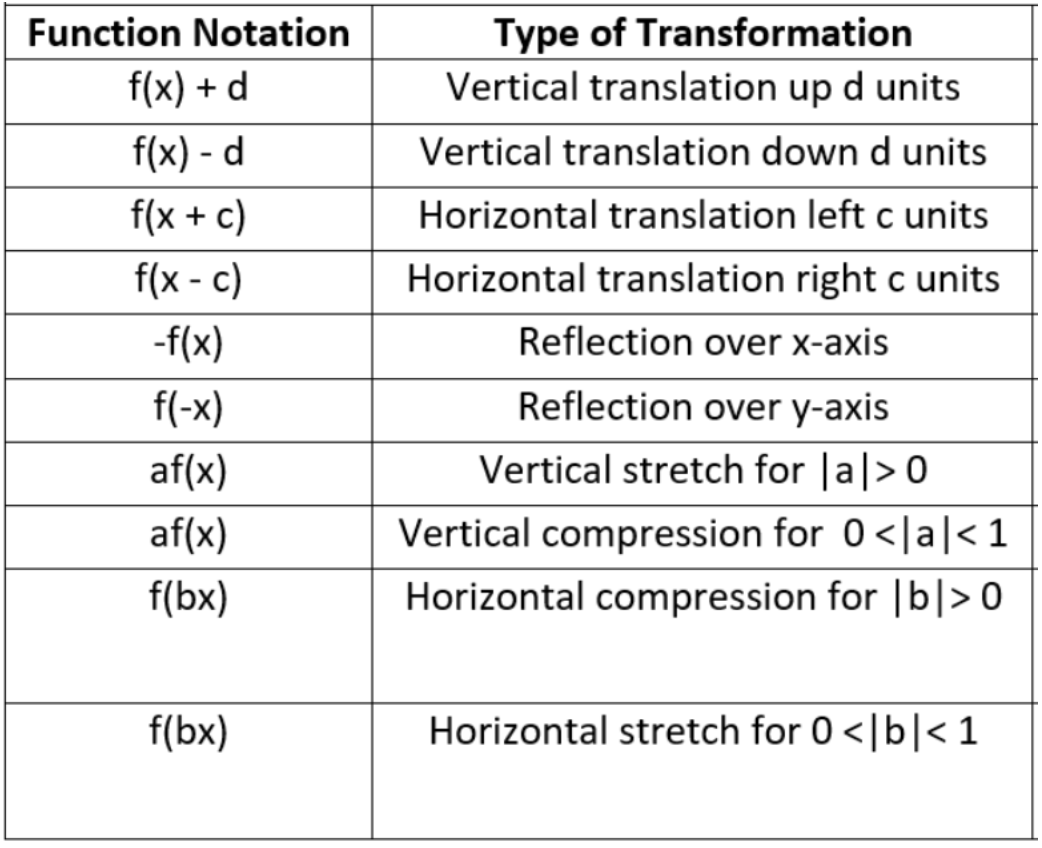
Exam Tip
You are expected to know all these possible transformations which can be applied to functions, so make sure you know them all.

