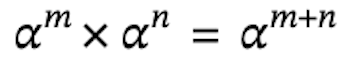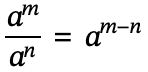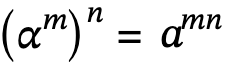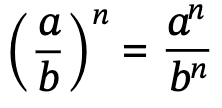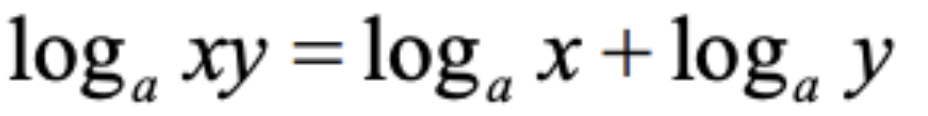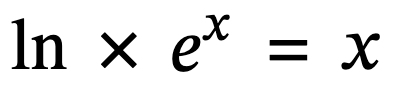Exponents and Logarithms
Exponents and Logarithms
Laws of Exponents
Multiplication with exponents
- If numbers have the same base and they are multiplying each other, you are able to add the exponents.
Division with exponents
- If numbers have the same base and they are dividing each other, you are able to subtract the exponents.
Expansion with exponents
- If there are brackets around a number with an exponent, and the value outside the bracket is an exponent, the exponents multiply with each other.
Negative exponents
- The value of the negative exponent becomes positive, and then you divide 1 by the number.
Further expansion with exponents
- If there are brackets around a number with an exponent, and the number is a fraction, and the value outside the bracket is an exponent, the exponent outside the brackets becomes the exponent for both the denominator and the numerator of the fraction.
Exam Tips
- You will be required to carry out multiple calculations with the laws of indices. Generally, the IB rarely asks only for an exponent solution. Knowledge of this topic is necessary for application to other topics (e.g. logarithms).
- Take your time and apply each law individually.
- Work with numbers first and then with algebra.
- Index laws only work with terms that have the same base, so be sure to manipulate the base of the term before using any of the index laws if necessary.
- Changing the base means rewriting the number as an exponent with the base you need.
- These laws are not in the formula booklet so you must remember them.
Logarithms
General formula of logarithms
- This formula is included in the formula book.
- Any time "a" is larger than "b", the answer will be a fraction.
- Any log "without" a written base is base 10.
- Trick: to find x, think of it as such: "What power of x would give me b?"
Adding logarithms
- You can multiply the "b" value of the logarithm if both logarithms have the same base and are adding together.
- This formula is included in the formula book.
Subtracting logarithms
- You can divide the "b" value of the logarithm if both logarithms have the same base and are subtracting together.
- This formula is included in the formula book.
Exponents with logarithms
- You can shift the exponent on the "b" value of the logarithm to the left of the logarithm, effectively multiplying the exponent with the logarithm.
- This is great to remove exponents; you do so by dividing the equation on both sides (after shifting it to the left).
- This formula is included in the formula book.
Natural logarithms
- "ln" is log base "e".
- When "ln" and "e" are to the power of each other, they cancel each other out.
- The same rules of logarithms apply to natural logarithms (e.g. multiplication).

Author: Felipe Rodrigues
Contact: fr1@stpauls.br