Sequences and Series

Index

• The letter u indicates the position of the term.
• Deductive definition: in terms of n.
• Inductive definition: in terms of previous term.
• In an inductive sequence, the n value you plug into is the previous value: e.g., to find the second value in the sequence you plug the first value in the list.
• Sigma notation is used to find the sum of the terms in a sequence. To solve, access your GDC and plug in the sequence.

Arithmetic sequences

• Adds the same number every time.
• Also called linear sequence.
• Common difference = d = u₂ – u₁.
• General formula for u at position n:
  
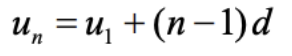
• General formula for sum n terms:
  

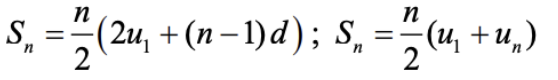
Geometric sequences

• Can also be called exponential sequence
• Multiplies by the same number every time (called r)
• Common ratio = r = u2 divided by u1, or u3 divided by u2, etc.
• General formula for u at position n:
  
• General formula for sum n terms:
  
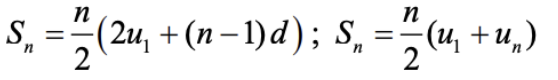
• General tip: you will need to use logarithms to solve for n

Infinite geometric series

• When the common ratio is smaller than 1
• Serie goes to infinity
• Common ratio = r = u2 divided by u1, or u3 divided by u2, etc.
• General formula for sum n terms: